問1問題を読み、クイズに答えましょう。
日本のある年の、二人以上の世帯について貯蓄現在高階級別の世帯分布をみると、4000万円以上の世帯は11.4%、100万円未満の世帯は10.3%、平均値は1798 万円でした。
このことから、どのような分析ができますか?適切なものを1つ選びましょう。

- ①平均値は1798 万円であるから、日本人の約半数の世帯の貯蓄高が1798 万円以上である。
- ②平均値は1798 万円でも、日本人の約半数の世帯の貯蓄高が1798 万円以上かどうかは分からない。標準偏差を調べれば、約半数の世帯の貯蓄高が1798 万円以上かどうか分かる。
- ③平均値は1798 万円でも、日本人の約半数の世帯の貯蓄高が1798 万円以上かどうかは分からない。相関係数を調べれば、約半数の世帯の貯蓄高が1798 万円以上かどうか分かる。
- ④平均値は1798 万円でも、日本人の約半数の世帯の貯蓄高が1798 万円以上かどうかは分からない。中央値を調べれば、約半数の世帯の貯蓄高が1798 万円以上かどうか分かる。
正解:④
解説
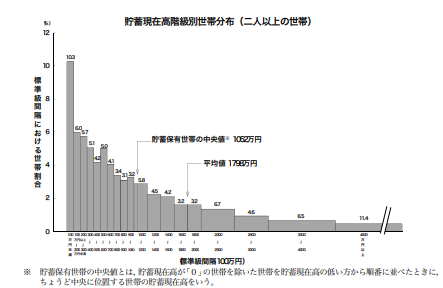
選択肢①は、平均値だけでは、分布は分からないため、不正解。
二人以上の世帯について貯蓄現在高階級別の世帯分布をみると、平均値(1798 万円)を下回る世帯が 約3分の2(67. 6%)を占め、貯蓄現在高の低い階級に偏ったものとなっています。
選択肢②は、平均値と標準偏差では、分布は分からないため、不正解。
標準偏差では「散らばりの度合い」すなわち、平均値からどれくらい離れているかが分かります。
選択肢③は、平均値と相関係数では、分布は分からないため、不正解。
相関係数で分かるのは、2つの変量の間の関係です。今回の変量は1つです。
選択肢④は、中央値が1052万円→半数の世帯の貯蓄高は1052万円以上であるため、正しい。
例えば、難しい試験で1人だけ100点の人がいると平均点は上がりますが、半数の人が平均点以上ではありません。
問2問題を読み、クイズに答えましょう。
下はあるクラスの生徒10人の身長と体重の散布図である。このクラスの平均的な体型と自分の体型を比較したい。私の身長が145cmのとき、このクラスの平均的な体型では何kgになるか。適切なものを1つ選びましょう。以下、i 番目の生徒の身長をxi、体重をyi、散布図中の赤い直線(破線)の方程式をy = ax + bとする。ただし、a,bは定数である。
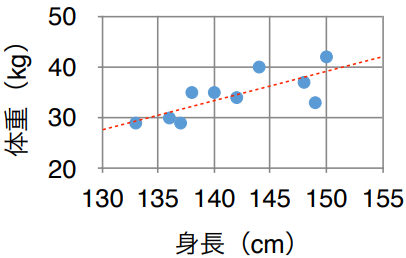
- ①身長の平均値をx、体重の平均値をyとすると、求める体重は、145 × y/x(kg)
- ②{y₁ − (ax₁ + b)} + {y₂ − (ax₂ + b)} + … + {y₁₀ − (ax₁₀ + b)}が0に近い値となるようにa, bを定めると、145a + b(kg)
- ③{y₁ − (ax₁ + b)}² + {y₂ − (ax₂ + b)}² + … + {y₁₀ − (ax₁₀ + b)}²が0に近い値となるようにa, bを定めると、145a + b(kg)
- ④|y₁ − (ax₁ + b)| + |y₂ − (ax₂ + b)| + … + |y₁₀ − (ax₁₀ + b)|が0に近い値となるようにa, bを定めると、145a + b(kg)
正解:③
解説
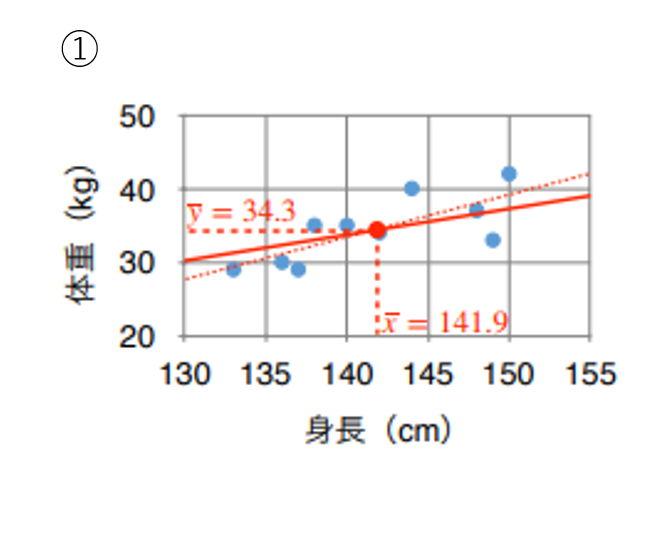
選択肢①は、点(x,y )と原点を結ぶ直線上の点になるため、不正解。
x = 141.9、y = 34.3 から、点 (141.9, 34.3) と原点を結ぶ直線は図のようになります。
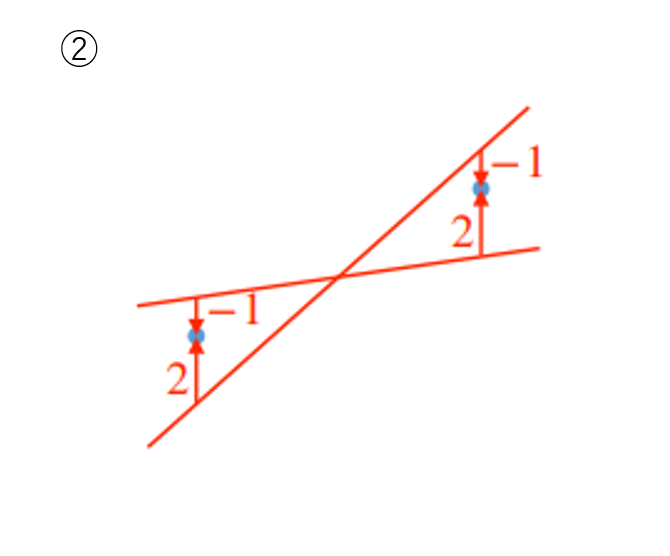
選択肢②は、正と負の誤差が差し引きされ、正しい直線が引けないため、不正解。
例えば、右の2つの直線は、2点との誤差の和は一致します。
また、正と負の誤差が差し引きされるので、点と直線が離れていても誤差の和が0になる場合があります。
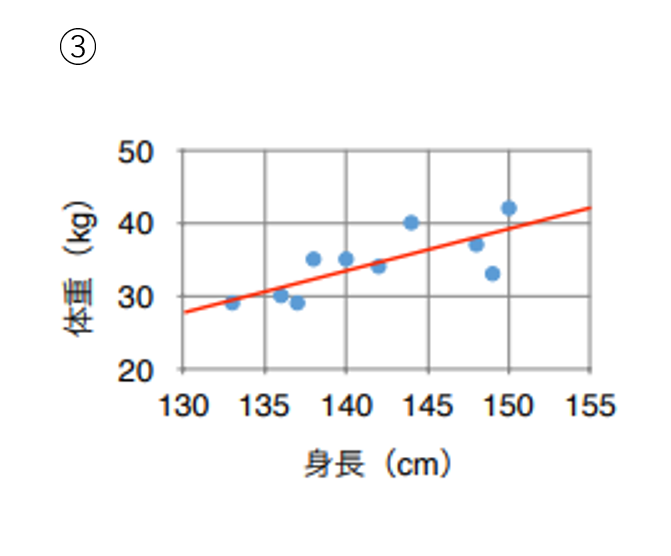
選択肢③は、正しい。この直線を回帰直線といい、求める方法を最小二乗法という。
2乗の和を求めるのは、分散・標準偏差と同じ原理です。
平均値からの距離が最小になるように定めます。
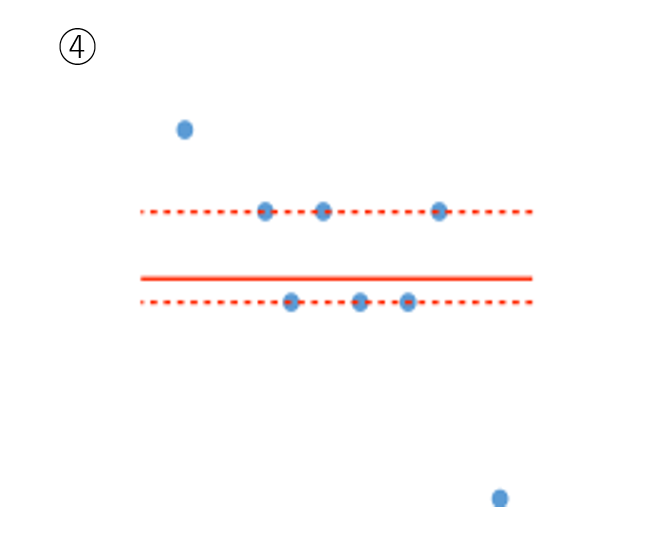
選択肢④は、負にならないので差し引きはされないが、最適解ではないため、不正解。
例えば、絶対値の和なら、右の3本の直線はどの直線を用いても、計算結果は同じ値になります。
しかし、2乗の和は、実線を用いた値が最小になります。
まとめ結果発表
たいへんよくできました
| 結果 |
|---|